零、前言
四边形不等式最早是 D.E.Knuth 在优化传统O(n3)区间dp求解最优二叉检索树为O(n2)所采用的方法,可惜原论文的证明跳跃性过强,阅读门槛较高. 不过随着算竞的发展,四边形不等式已经有了较为完备的可参考资料,本文进行介绍.
一、再看[石子合并]
石子合并是区间dp的经典入门问题,我们可以在O(n3)内求解,事实上,大部分的区间合并题目要么是O(n2)状态数,O(n)状态转移,要么是O(n^3)状态数,O(1)状态转移。
下面是原题链接以及AC代码
P1775 石子合并(弱化版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
const int N = 305;
int n, w[N], f[N][N];
int main() {
std::cin >> n;
for (int i = 1; i <= n; i ++) std::cin >> w[i];
for (int i = 2; i <= n; i ++) w[i] += w[i - 1];
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; i ++) f[i][i] = 0;
for (int len = 2; len <= n; len ++)
for (int l = 1; l <= n - len + 1; l ++) {
int r = l + len - 1;
for (int k = l; k < r; k ++)
f[l][r] = std::min(f[l][r], f[l][k] + f[k + 1][r] + w[r] - w[l - 1]);
}
std::cout << f[1][n];
return 0;
}
这种入门级区间dp问题太过简单,那我们为什么要再看这道题目呢?
我们以样例
5
1 3 1 4 2 5
为例,打表观察状态转移是否存在某种规律。
[l, r]代表区间,k[]代表状态转移时枚举的分割点集合,即f[l][r] = std::min(f[l][r], f[l][k] + f[k + 1][r] + w[r] - w[l - 1]);
状态转移时通过枚举这样的分割点集合我们可以计算出最优解为41
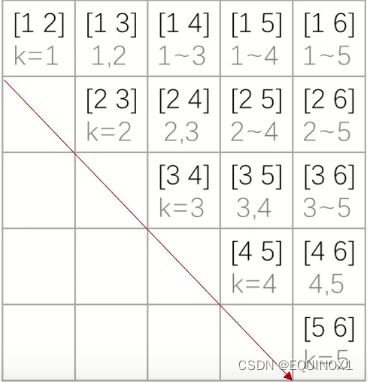
上图中每条副对角线的区间长度相同,从左下到右上长度递增。
下面是我们优化过的分割点集合,每个区间格子的分割点集合为**[左边格子最优划分点,下方格子最优划分点]**

我们以新的分割点集合进行区间dp,同样得出了最优解:41
我们尝试按照上述策略改写代码:
#include <bits/stdc++.h>
const int N = 305;
int n, w[N], f[N][N], p[N][N];
int main() {
std::cin >> n;
for (int i = 1; i <= n; i ++) std::cin >> w[i];
for (int i = 2; i <= n; i ++) w[i] += w[i - 1];
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; i ++) f[i][i] = 0, p[i][i] = i;
for (int len = 2; len <= n; len ++)
for (int l = 1, r; (r = l + len - 1) <= n; l ++) {
for (int k = p[l][r - 1]; k <= p[l + 1][r]; k ++)
if(f[l][r] > f[l][k] + f[k + 1][r] + w[r] - w[l - 1])
f[l][r] = f[l][k] + f[k + 1][r] + w[r] - w[l - 1], p[l][r] = k;
}
std::cout << f[1][n];
return 0;
}
我们发现通过了本题。

二者有何不同呢?
我们来看同样的题,只不过范围加强到了5000,二者的效果
2889. 再探石子合并 - AcWing题库
旧版写法:

新版写法:

可见,优化过的写法不仅正确且效率更高!
这里先说明一下结论:上面的优化方式为四边形不等式优化dp,将O(n3)的朴素区间合并优化到了O(n2),那么为什么可以这样优化,原理是什么?且听下回分解下面进行详述。
二、四边形不等式
2.1 四边形不等式
设 w(x, y)是定义在整数集合上的二元函数。若对于定义域上的任意整数 a,b,c,d,其中a <= b <= c <= d,都有:
w
(
a
,
d
)
+
w
(
b
,
c
)
≥
w
(
a
,
c
)
+
w
(
b
,
d
)
w(a, d) + w(b, c) \ge w(a, c) + w(b, d)
w(a,d)+w(b,c)≥w(a,c)+w(b,d)
我们称函数 w 满足四边形不等式。
2.2 定理(四边形不等式的另一种定义)
设 w(x, y)是定义在整数集合上的二元函数。若对于定义域上的任意整数 a,b,其中a < b ,都有:
w
(
a
,
b
+
1
)
+
w
(
a
+
1
,
b
)
≥
w
(
a
,
b
)
+
w
(
a
+
1
,
b
+
1
)
w(a, b+1) + w(a+1, b) \ge w(a, b) + w(a+1, b+1)
w(a,b+1)+w(a+1,b)≥w(a,b)+w(a+1,b+1)
我们称函数 w 满足四边形不等式。
证明:
只需证明定义和该定理互为充要条件。
- 证明定理必要性(1推2)
a < b => a < a + 1 <= b <= b + 1,则定理显然正确
- 证明定理充分性(2推1)
对于 a < c , 有 w ( a , c + 1 ) + w ( a + 1 , c ) ≥ w ( a , c ) + w ( a + 1 , c + 1 ) 对于 a + 1 < c , 有 w ( a + 1 , c + 1 ) + w ( a + 2 , c ) ≥ w ( a + 1 , c ) + w ( a + 2 , c + 1 ) 两式相加,得到 w ( a , c + 1 ) + w ( a + 2 , c ) ≥ w ( a , c ) + w ( a + 2 , c + 1 ) 迭代下去, a + 2 < c 、 a + 3 < c 不妨把 a + k < c 替换为 b < c ,更进一步替换为 a ≤ b ≤ c ( 每迭代一次 b 就 + 1 ,会覆盖 [ a , c ] ) 得到 ∀ a ≤ b ≤ c ,有 w ( a , c + 1 ) + w ( b , c ) ≥ w ( a , c ) + w ( b , c + 1 ) 同理,对 c 迭代, a ≤ b ≤ c + 1 ≤ c + 2 , w ( a , c + 2 ) + w ( b , c + 1 ) ≥ w ( a , c + 1 ) + w ( b , c + 2 ) 两式相加 : w ( a , c + 2 ) + w ( b , c ) ≥ w ( a , c ) + w ( b , c + 2 ) 那么不断迭代下去,取 d = c + k , d 能覆盖 [ c , + ∞ ] 则有 w ( a , d ) + w ( b , c ) ≥ w ( a , c ) + w ( b , d ) , a ≤ b ≤ c ≤ d \begin{align} & 对于 a\lt c, 有w(a, c+1) + w(a+1, c) \ge w(a, c) + w(a+1, c+1) \\ \\ & 对于 a + 1\lt c, 有w(a+1, c+1) + w(a+2, c) \ge w(a+1, c) + w(a+2, c+1) \\ \\ & 两式相加,得到 w(a, c + 1) + w(a + 2, c) \ge w(a, c) + w(a+2, c + 1) \\ \\ & 迭代下去,a + 2 \lt c、a + 3 \lt c \\ \\ & 不妨把a+k \lt c 替换为 b \lt c,更进一步替换为 a \le b \le c(每迭代一次b就+1,会覆盖[a, c])\\ \\ & 得到\forall a \le b \le c,有w(a, c+1)+w(b,c)\ge w(a,c)+w(b,c+1) \\ \\ & 同理,对c迭代,a \le b \le c+1 \le c+2,w(a, c+2)+w(b,c+1)\ge w(a,c+1)+w(b,c+2) \\ \\ & 两式相加:w(a,c+2)+w(b,c)\ge w(a,c)+w(b,c+2) \\ \\ & 那么不断迭代下去,取d = c + k,d能覆盖[c, +\infty] \\ \\ & 则有w(a, d) + w(b, c) \ge w(a, c) + w(b, d), a\le b\le c\le d \end{align} 对于a<c,有w(a,c+1)+w(a+1,c)≥w(a,c)+w(a+1,c+1)对于a+1<c,有w(a+1,c+1)+w(a+2,c)≥w(a+1,c)+w(a+2,c+1)两式相加,得到w(a,c+1)+w(a+2,c)≥w(a,c)+w(a+2,c+1)迭代下去,a+2<c、a+3<c不妨把a+k<c替换为b<c,更进一步替换为a≤b≤c(每迭代一次b就+1,会覆盖[a,c])得到∀a≤b≤c,有w(a,c+1)+w(b,c)≥w(a,c)+w(b,c+1)同理,对c迭代,a≤b≤c+1≤c+2,w(a,c+2)+w(b,c+1)≥w(a,c+1)+w(b,c+2)两式相加:w(a,c+2)+w(b,c)≥w(a,c)+w(b,c+2)那么不断迭代下去,取d=c+k,d能覆盖[c,+∞]则有w(a,d)+w(b,c)≥w(a,c)+w(b,d),a≤b≤c≤d
2.3 一维线性dp 的四边形不等式优化
2.3.1 概念定理及证明
对于形如
f
(
i
)
=
m
i
n
0
≤
j
≤
i
(
f
(
i
)
+
v
a
l
(
j
,
i
)
)
f(i) = min_{0\le j\le i}(f(i) + val(j, i))
f(i)=min0≤j≤i(f(i)+val(j,i))
的状态转移方程,记p(i)为令f(i)取到最小值的 j 的值,即p(i)是f(i)的最优决策。若p在[1,N]上单调不减(非严格单调递增), 则称f具有决策单调性.
**定理:**在状态转移方程
f
(
i
)
=
m
i
n
0
≤
j
≤
i
(
f
(
i
)
+
v
a
l
(
j
,
i
)
)
f(i) = min_{0\le j\le i}(f(i) + val(j, i))
f(i)=min0≤j≤i(f(i)+val(j,i))
中,若函数val满足四边形不等式,则f具有决策单调性.
证明:
∀
i
∈
[
1
,
N
]
,
∀
j
∈
[
0
,
p
(
i
)
−
1
]
,
根据
p
(
i
)
的最优性
,
有
:
f
(
p
(
i
)
)
+
v
a
l
(
p
(
i
)
,
i
)
≤
f
(
j
)
+
v
a
l
(
j
,
i
)
…
①
∀
i
′
∈
[
j
+
1
,
N
]
,
因为
v
a
l
满足四边形不等式
,
有
:
v
a
l
(
j
,
i
′
)
+
v
a
l
(
p
(
i
)
,
i
)
≥
v
a
l
(
j
,
i
)
+
v
a
l
(
p
(
i
)
,
i
′
)
移项
v
a
l
(
p
(
i
)
,
i
′
)
−
v
a
l
(
p
(
i
)
,
i
)
≤
v
a
l
(
j
,
i
′
)
−
v
a
l
(
j
,
i
)
…
②
①
+
②
:
f
(
p
(
i
)
)
+
v
a
l
(
p
(
i
)
,
i
′
)
≤
f
(
j
)
+
v
a
l
(
j
,
i
)
,
其中
i
∈
[
1
,
N
]
,
l
∈
[
0
,
p
(
i
)
−
1
]
故
f
具有决策单调性
证毕
\begin{align} & \forall i \in [1,N], \forall j \in [0, p(i) - 1],根据p(i)的最优性,有:\\ \\ & f(p(i)) + val(p(i),i)\le f(j)+val(j,i) \dots ①\\ \\ & \forall i' \in [j + 1,N], 因为val满足四边形不等式,有:\\ \\ & val(j, i')+val(p(i),i)\ge val(j, i)+val(p(i),i')\\ \\ & 移项 \\ \\ & val(p(i),i')-val(p(i),i)\le val(j,i')-val(j,i) \dots ②\\ \\ & ①+②:\\ \\ & f(p(i))+val(p(i),i')\le f(j)+val(j,i),其中i \in [1,N],l \in [0, p(i) - 1]\\ \\ & 故\ f \ 具有决策单调性 \\ \\ & 证毕 \end{align}
∀i∈[1,N],∀j∈[0,p(i)−1],根据p(i)的最优性,有:f(p(i))+val(p(i),i)≤f(j)+val(j,i)…①∀i′∈[j+1,N],因为val满足四边形不等式,有:val(j,i′)+val(p(i),i)≥val(j,i)+val(p(i),i′)移项val(p(i),i′)−val(p(i),i)≤val(j,i′)−val(j,i)…②①+②:f(p(i))+val(p(i),i′)≤f(j)+val(j,i),其中i∈[1,N],l∈[0,p(i)−1]故 f 具有决策单调性证毕
2.3.2 算法原理
那么我们优化前, f求解的总时间复杂度为O(n^2),优化后可以降低到O(nlogn)
考虑初态f(1)为初始状态显然已知,且p(1)已知,二者具体值据题目而定
当我们计算f(i)时,如果已知p(i),那么可以O(1)计算出f(i) = f(p(i)) + val(p(i), i)
由于初态已知,我们考虑在计算出f(i)后,能否快速判断出f(i)可以作为哪些f(i')的最优决策点呢?
任意时刻p应该满足如下形式
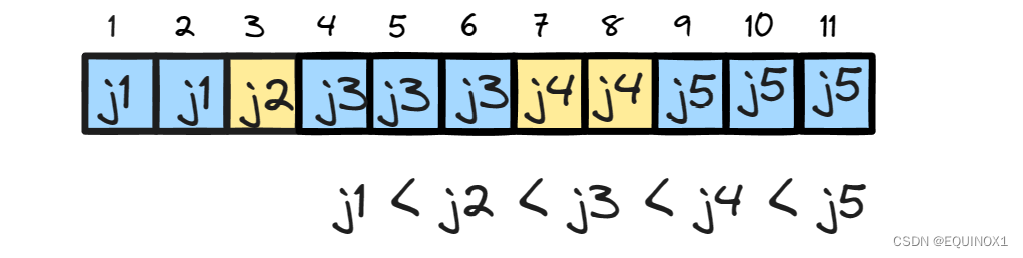
当我们计算出f(i),那么p中存在位置j使得 j 之前 p值都小于i,j以及j之后均不小于i,所以我们可以找到j并更新j之后的p值为i
问题有两个:
- 如何快速找到
j - 如何快速更新
j以后的值为i
解决方式:用队列存储(j,l,r)三元组来替代p数组,即(l,r)内的最优决策都是j
那么上面例图可表:
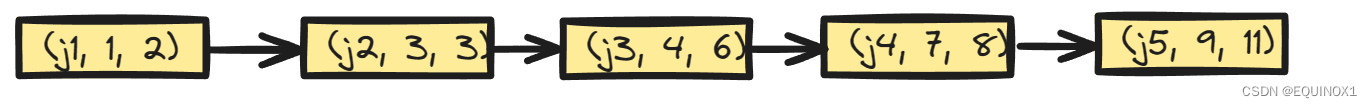
假如我们计算出了f(i),我们需要更新上面的p为如下样子,其中j1 < j2 < j3 < i
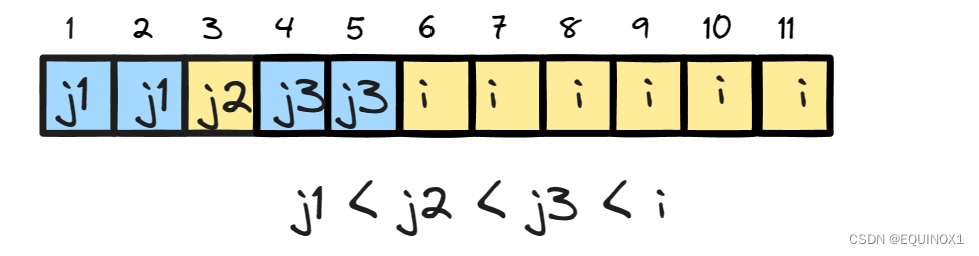
上面调整的过程在队列实现p时是如何表现的呢?
我们从队尾向前枚举三元组
对(j5, 9, 11)而言,我们判断f(j5)+val(j5,9) > f(i)+val(i,9),将其弹出,由于p单调性[10, 11]不再检测
对(j4, 7, 8)而言,我们判断f(j5)+val(j5,7) > f(i)+val(i,7),将其弹出
对(j3, 4, 6)而言,我们判断**f(j3)+val(j3,6) < f(i)+val(i,6)(注意这里是6不是4哦)**说明[4, 6]可能一部分j3更优一部分i更优,说明p在[4, 6]内分为两段分别为j3和i具有两段性,我们二分找到分割点,在上面的例子中是找到了5为分割点,我们修改(j3, 4, 6)为(j3, 4, 5),然后插入(i,6,11)
另外,队列中没有必要保存小于p[1 ~ i-1]的部分,我们可以通过检查队头来排除掉过时的决策。这样就可以像许多单调队列问题一样,直接取队头为最优决策
2.3.2 算法流程
- 对于每个
i ∈ [1, N],我们执行以下操作: - 检查队头:如果队头
r = i - 1,就弹出队头, 否则令队头l = 0 - 取队头的
j作为p(i)对f(i)进行更新 - 插入
i到队尾- 弹出队尾所有比左端点
i更差的三元组 - 遇到左端点比
i更优的三元组,直接插入i的三元组 - 否则,在该三元组上二分分段点,调整该三元组然后调整该三元组,插入
i三元组
- 弹出队尾所有比左端点
2.3.3 OJ练习
原题链接
[P1912 NOI2009] 诗人小G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路分析
我们考虑定义状态f(i)为前i个句子排列后的最小不协调度
那么有状态转移方程:
f
(
i
)
=
m
i
n
1
≤
j
≤
i
(
f
(
j
)
+
p
o
w
(
a
b
s
(
i
−
j
+
s
(
j
,
i
)
)
,
P
)
)
这里
s
(
j
,
i
)
为前
[
j
,
i
]
内句子的长度和
令
v
a
l
(
i
,
j
)
=
a
b
s
(
i
−
j
+
s
(
j
,
i
)
)
f(i) = min_{1 \le j \le i}(f(j) + pow(abs(i - j + s(j, i)), P)) \\ 这里s(j, i)为前[j, i]内句子的长度和 \\ 令val(i, j) = abs(i - j + s(j, i))
f(i)=min1≤j≤i(f(j)+pow(abs(i−j+s(j,i)),P))这里s(j,i)为前[j,i]内句子的长度和令val(i,j)=abs(i−j+s(j,i))
我们分析val是否满足四边形不等式.
只需证:val(j, i + 1) + val(j + 1, i) >= val(j, i) + val(j + 1, i + 1)
只需证:val(j + 1, i) - val(j + 1, i + 1) >= val(j, i) - val(j, i + 1)
令:
u = (sum(i) + i) - (sum(j) + j) - (L + 1)
v = (sum(i) + i) - (sum(j + 1) + j + 1) - (L + 1)
上式即证:|v| ^ P - |v + len(i + 1) + 1|^P >= |u| ^ P - |u + len(i + 1) + 1|^P
我们构造同构函数:g(x) = |x| ^ p - |x + c| ^ p
由于u >= v, 我们只需证g(x)单调递减
下面按P奇偶性分情况讨论,然后每种情况再分(-∞, c], (c, 0], (0, +∞)三个区间讨论
求导不难发现导数始终为负数,所以得证,val满足四边形不等式
所以就可以优化我们的朴素一维线性dp啦
本题的坑:
- 输出格式,空格,换行等
- 爆
long long,__int128,要用long double(long double会有long long转long double的精度损失,int则不会)或者求方案的时候再重新用long long计算下答案
AC代码:
#include <bits/stdc++.h>
using i64 = long long;
using LD = long double;
const int N = 1e5 + 10;
int n, L, P, h, t, p[N];
int s[N];
LD f[N];
std::string words[N];
const std::string border(20, '-');
struct node {
int j, l, r;
} q[N];
LD val(int j, int i) {
LD res = 1, a = abs(s[i] - s[j] + i - j - 1 - L);
for (int b = P; b; b >>= 1, a *= a)
if (b & 1) res *= a;
return res + f[j];
}
void insert(int i) {
int ed = -1;
while (h < t && val(q[t - 1].j, q[t - 1].l) >= val(i, q[t - 1].l))
ed = q[-- t].l;
if (h < t && val(q[t - 1].j, q[t - 1].r) >= val(i, q[t - 1].r)) {
int l = q[t - 1].l, r = q[t - 1].r;
while (l < r) {
int mid = l + r >> 1;
val(q[t - 1].j, mid) >= val(i, mid) ? r = mid : l = mid + 1;
}
q[t - 1].r = r - 1;
ed = r;
}
if (~ed)
q[t ++] = { i, ed, n };
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int _ = 1;
std::cin >> _;
while (_ --) {
std::cin >> n >> L >> P;
for (int i = n; i >= 1; i --)
std::cin >> words[i];
for (int i = 1; i <= n; i ++)
s[i] = words[i].size() + s[i - 1];
h = t = 0;
q[t ++] = { 0, 1, n };
for (int i = 1; i <= n; i ++ ) {
f[i] = val(p[i] = q[h].j, i);
while (h < t && q[h].r <= i) h ++;
if (h < t)
q[h].l = i + 1;
insert(i);
}
if (f[n] > 1e18) std::cout << "Too hard to arrange\n";
else {
std::cout << (i64)f[n] << '\n';
for (int i = n; i; i = p[i]) {
for (int j = i; j > p[i]; j --) {
std::cout << words[j];
if (j > p[i] + 1) std::cout << ' ';
}
std::cout << '\n';
}
}
std::cout << border;
if (_)
std::cout << '\n';
}
return 0;
}
2.4 二维区间dp 的四边形不等式优化
2.4.1 概念定理及证明
区间dp问题,如"石子合并",我们有如下形式的状态转移方程:
f
(
i
,
j
)
=
m
i
n
i
≤
k
≤
j
{
f
(
i
,
k
)
+
f
(
k
+
1
,
j
)
+
w
(
i
,
j
)
}
f(i,j)=min_{i\le k\le j}\{f(i,k)+f(k+1,j)+w(i,j)\}
f(i,j)=mini≤k≤j{f(i,k)+f(k+1,j)+w(i,j)}
定理
在状态转移方程
f
(
i
,
j
)
=
m
i
n
i
≤
k
≤
j
{
f
(
i
,
k
)
+
f
(
k
+
1
,
j
)
+
w
(
i
,
j
)
}
f(i,j)=min_{i\le k\le j}\{f(i,k)+f(k+1,j)+w(i,j)\}
f(i,j)=mini≤k≤j{f(i,k)+f(k+1,j)+w(i,j)}
中**(特别的,f(i, i) = w(i, i) = 0, f(i, i + 1) = w(i, i + 1)),**如果下面两个条件成立:
w满足四边形不等式- 对任意
a <= b <= c <= d,有w(a, d) >= w(b, c)
那么F也满足四边形不等式
证明:
当i + 1 = j时,f(i, j + 1) + f(i + 1, j) = f(i, i + 2) + f(i + 2, i + 2) = f(i, i + 2)
若证f(i, j + 1) + f(i + 1, j) >= f(i, j) + f(i + 1, j + 1),即证f(i, j + 1) >= f(i, j) + f(i + 1, j + 1)
f(i, i + 2)的决策集合:{i, i + 1}
-
若
f(i, i + 2)的最优决策为i + 1:- 则
f(i, i + 2) = f(i, i + 1) + f(i, i + 2) + w(i, i + 2) >= f(i, i + 1) + f(i + 1, i + 2) - 即
f(i, j + 1) >= f(i, j) + f(i + 1, j + 1)
- 则
-
若
f(i, i + 2)的最优决策为i:- 则
f(i, i + 2) = f(i, i) + f(i + 1, i + 2) + w(i, i + 2) = w(i + 1, i + 2) + w(i, i + 2) >= w(i + 1, i + 2) + w(i, i + 1) = f(i + 1, i + 2) + f(i, i + 1) - 即
f(i, j + 1) >= f(i, j) + f(i + 1, j + 1)
- 则
故得证.
故当i + 1 = j时,f(i, j),满足四边形不等式
下面用数学归纳法,假设j - i < k (k >= 2)时,四边形不等式对f(i,j)成立,下面只需证j - i = k时也成立:
假设f(i, j + 1)以x为最优决策,f(i + 1, j)以y为最优决策.
- 若
x <= y, 则有i <= x <= y < j-
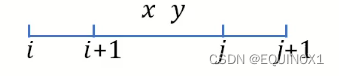
-
f(i, j + 1) + f(i + 1, j) = f(i, x) +f(x + 1, j + 1)+ w(i, j + 1) + f(i + 1, y) +f(y + 1, j)+ w(i + 1, j),对于f(i, j)和f(i + 1, j + 1),x, y不一定是最优决策(说明下面可以放缩了) -
f(i, j) + f(i + 1, j + 1) <= f(i, x) +f(x + 1, j)+ w(i, j) + f(i + 1, y) +f(y + 1, j + 1)+ w(i + 1, j + 1) -
根据假设,
f(x + 1, j + 1) + f(y + 1, j) >= f(x + 1, j) + f(y + 1, j + 1),因为j - (x + 1) < j - i = k
-
由于
w满足四边形不等式,所以**w(i, j + 1) + w(i + 1, j) >= w(i, j) + w(i + 1, j + 1)** -
结合
2. 3. 4. 5.可以推出**f(i, j + 1) + f(i + 1, j) >= f(i, j) + f(i + 1, j + 1)**,得证
-
- 若
y < x, 则有i + 1 <= y < x <= j-
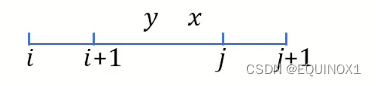
-
f(i, j + 1) + f(i + 1, j) =f(i, x)+ f(x + 1, j + 1) + w(i, j + 1) +f(i + 1, y)+ f(y + 1, j) + w(i + 1, j),对于f(i, j)和f(i + 1, j + 1),y, x不一定是最优决策(说明下面可以放缩了) -
f(i, j) + f(i + 1, j + 1) >=f(i, y)+ f(y + 1, j) + w(i, j) +f(i + 1, x)+ f(x + 1, j + 1) + w(i + 1, j + 1) -
根据假设,
f(i, x) + f(i + 1, y) >= f(i, y) + f(i + 1, x),因为x - 1 - i < j - i = k
-
由于
w满足四边形不等式,所以**w(i, j + 1) + w(i + 1, j) >= w(i, j) + w(i + 1, j + 1)** -
结合
2. 3. 4. 5.可以推出**f(i, j + 1) + f(i + 1, j) >= f(i, j) + f(i + 1, j + 1)**,得证
-
故f满足四边形不等式,得证
定理(决策单调性)
在状态转移方程
f
(
i
,
j
)
=
m
i
n
i
≤
k
≤
j
{
f
(
i
,
k
)
+
f
(
k
+
1
,
j
)
+
w
(
i
,
j
)
}
f(i,j)=min_{i\le k\le j}\{f(i,k)+f(k+1,j)+w(i,j)\}
f(i,j)=mini≤k≤j{f(i,k)+f(k+1,j)+w(i,j)}
中(特别的,f(i, i) = w(i, i) = 0, f(i, i + 1) = w(i, i + 1)), 记p(i, j)为f(i, j)取到最小值的k值
如果f满足四边形不等式, 那么对于任意i < j, 有**p(i, j - 1) <= p(i, j) <= p(i + 1, j).**
证明:
证明p(i, j) <= p(i + 1, j):
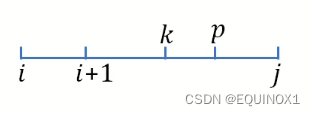
为方便起见,p = p(i, j),对于任意的i < k <= p,因为f满足四边形不等式:
f(i, p) + f(i + 1, k) >= f(i, k) + f(i + 1, p)
移项可得:
f(i + 1, k) - f(i + 1, p) >= f(i, k) - f(i, p)
根据p的最优性,有:
f(i, k) + f(k + 1, j) >= f(i, p) + f(p + 1, j)
因而
(
f
(
i
+
1
,
k
)
+
f
(
k
+
1
,
j
)
+
w
(
i
+
1
,
j
)
)
−
(
f
(
i
+
1
,
p
)
+
f
(
p
+
1
,
j
)
+
w
(
i
+
1
,
j
)
)
=
(
f
(
i
+
1
,
k
)
−
f
(
i
+
1
,
p
)
)
+
(
f
(
k
+
1
,
j
)
−
f
(
p
+
1
,
j
)
)
≥
(
f
(
i
,
k
)
−
f
(
i
,
p
)
)
+
(
f
(
k
+
1
,
j
)
−
f
(
p
+
1
,
j
)
)
=
(
f
(
i
,
k
)
+
f
(
k
+
1
,
j
)
)
−
(
f
(
i
,
p
)
+
f
(
p
+
1
,
j
)
)
≥
0
\begin{align} &\ \ \ \ \ (f(i + 1, k) + f(k + 1, j) + w(i + 1, j)) - (f(i + 1, p) + f(p + 1, j) + w(i + 1, j)) \\ &= (f(i + 1, k) - f(i + 1, p)) + (f(k + 1, j) - f(p + 1, j)) \\ &\ge (f(i, k) - f(i, p)) + (f(k + 1, j) - f(p + 1, j)) \\ &= (f(i, k) + f(k + 1, j)) - (f(i, p) + f(p + 1, j)) \\ &\ge 0 \end{align}
(f(i+1,k)+f(k+1,j)+w(i+1,j))−(f(i+1,p)+f(p+1,j)+w(i+1,j))=(f(i+1,k)−f(i+1,p))+(f(k+1,j)−f(p+1,j))≥(f(i,k)−f(i,p))+(f(k+1,j)−f(p+1,j))=(f(i,k)+f(k+1,j))−(f(i,p)+f(p+1,j))≥0
故,对于f(i + 1, j)而言p比任何k ∈ [1, p]更优, 即p(i, j) <= p(i + 1, j)
证明p(i, j - 1) <= p(i, j):
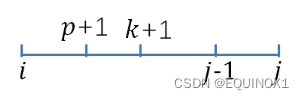
为方便起见,p = p(i, j), 取i <= p < k < j - 1(p = j - 1的情况不用证明), 因为f满足四边形不等式:
f(p + 1, j) + f(k + 1, j - 1) >= f(p + 1, j - 1) + f(k + 1, j)
移项可得:
f(k + 1, j - 1) - f(p + 1, j - 1) >= f(k + 1, j) - f(p + 1, j)
根据p的最优性,有:
f(i, k) + f(k + 1, j) >= f(i, p) + f(p + 1, j)
因而
(
f
(
i
,
k
)
+
f
(
k
+
1
,
j
−
1
)
+
w
(
i
,
j
−
1
)
)
−
(
f
(
i
,
p
)
+
f
(
p
+
1
,
j
−
1
)
+
w
(
i
,
j
−
1
)
)
=
(
f
(
i
,
k
)
−
f
(
i
,
p
)
)
+
(
f
(
k
+
1
,
j
−
1
)
−
f
(
p
+
1
,
j
−
1
)
)
≥
(
f
(
i
,
k
)
−
f
(
i
,
p
)
)
+
(
f
(
k
+
1
,
j
−
1
)
−
f
(
p
+
1
,
j
)
)
=
(
f
(
i
,
k
)
+
f
(
k
+
1
,
j
)
)
−
(
f
(
i
,
p
)
+
f
(
p
+
1
,
j
)
)
≥
0
\begin{align} &\ \ \ \ \ (f(i, k) + f(k + 1, j - 1) + w(i, j - 1)) - (f(i, p) + f(p + 1, j - 1) + w(i, j - 1)) \\ &= (f(i, k) - f(i, p)) + (f(k + 1, j - 1) - f(p + 1, j - 1)) \\ &\ge (f(i, k) - f(i, p)) + (f(k + 1, j - 1) - f(p + 1, j)) \\ &= (f(i, k) + f(k + 1, j)) - (f(i, p) + f(p + 1, j)) \\ &\ge 0 \end{align}
(f(i,k)+f(k+1,j−1)+w(i,j−1))−(f(i,p)+f(p+1,j−1)+w(i,j−1))=(f(i,k)−f(i,p))+(f(k+1,j−1)−f(p+1,j−1))≥(f(i,k)−f(i,p))+(f(k+1,j−1)−f(p+1,j))=(f(i,k)+f(k+1,j))−(f(i,p)+f(p+1,j))≥0
故,对于f(i, j - 1)而言p比任何k ∈ (p, j - 1)更优, 即p(i, j - 1) <= p
故如果f满足四边形不等式, 那么对于任意i < j, 有**p(i, j - 1) <= p(i, j) <= p(i + 1, j).**, 得证.
那么说了这么多, 用了四边形不等式优化后我们f求解的时间复杂度为多少?
下面是改进后的c++伪代码
for (int len = 2; len <= n; len ++)
for (int l = 1, r; (r = l + len - 1) <= n; l ++) {
for (int k = p[l][r - 1]; k <= p[l + 1][r]; k ++)
if(f[l][r] > f[l][k] + f[k + 1][r] + w[l][r])
f[l][r] = f[l][k] + f[k + 1][r] + w[l][r], p[l][r] = k;
}
-
对于每个
len,计算l和k的循环总次数k 循环次数 p[l + 1, r] - p[l, r - 1] + 1, r = l + len - 1l = 1, k 循环次数 = p(2, len) - p(1, len - 1) + 1l = 2, k循环次数 = p(3, 2 + len) - p(1, 1 + len) + 1...l = n + 1 - len, k 循环次数 = p(n + 2 - len, n) - p(n + 1 - len, n - 1) + 1累加 l 和 k循环次数 = p(n + 2 - len, n) - p(1, len - 1) + n - len + 1我们记 S(len) = p(n + 2 - len, n) - p(1, len - 1) + n - len + 1
-
len = 2时, S(2) = p(n, n) - p(1, 1) + n - 1 = 2n - 2
-
len = 3时, S(3) = p(n, n) - p(1, 1) + n - 2 = 2n - 3
-
…
-
len = n时, S(n) = p(n, n) - p(1, 1) + n - n + 1 = n - 1
-
∑ i = 2 n S ( i ) = 2 n − 2 + 2 n − 3 + . . . + n − 1 = 3 n ( n − 1 ) 2 \sum_{i=2}^{n}S(i) = 2n - 2 + 2n - 3 + ... + n - 1 = \frac{3n(n-1)}{2} i=2∑nS(i)=2n−2+2n−3+...+n−1=23n(n−1)
-
故时间
l 和 k两层循环的时间复杂度为O(n),算法总体时间复杂度为O(n^2)
2.4.2 OJ练习
原题链接
2889. 再探石子合并 - AcWing题库
思路分析
f(l, r)为区间[l, r]内石子合并的最小代价, 那么 f(l, r) = min{f(l, k) + f(k + 1, r) + w(l, r)},其中w(l, r)为[l, r]内石子重量之和
任意l < r
w(l, r + 1) + w(l + 1, r) = s(r + 1) - s(l - 1) + s(r) - s(l)①
w(l, r) + w(l + 1, r + 1) = s(r) - s(l - 1) + s(r + 1) - s(l)②
①-② = 0, 说明w(l, r)符合四边形不等式进而推出f符合四边形不等式进而推出p具有决策单调性
直接写优化后的代码即可
AC代码
#include <bits/stdc++.h>
const int N = 5005;
int f[N][N], p[N][N], s[N], n;
int main() {
std::cin >> n;
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i ++)
std::cin >> s[i], s[i] += s[i - 1], f[i][i] = 0, p[i][i] = i;
for(int len = 2; len <= n; len ++)
for(int l = 1, r; (r = l + len - 1) <= n; l ++)
for(int k = p[l][r - 1]; k <= p[l + 1][r]; k ++) {
if (f[l][r] > f[l][k] + f[k + 1][r] + s[r] - s[l - 1])
f[l][r] = f[l][k] + f[k + 1][r] + s[r] - s[l - 1], p[l][r] = k;
}
std::cout << f[1][n];
return 0;
}
三、其他练习
3.1 P1880 [NOI1995] 石子合并
原题链接
[P1880 NOI1995] 石子合并 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路分析
做这个题主要是想说明
- 只有最小值能用四边形不等式优化
- 但是最大值可以贪心优化,即区间最大值由两个端点最大值决定
-
f(l, r) = max(f(l, r - 1) + f(l + 1, r)) + w(l, r),即从两端选择 -
考虑长度为3时,显然成立
-
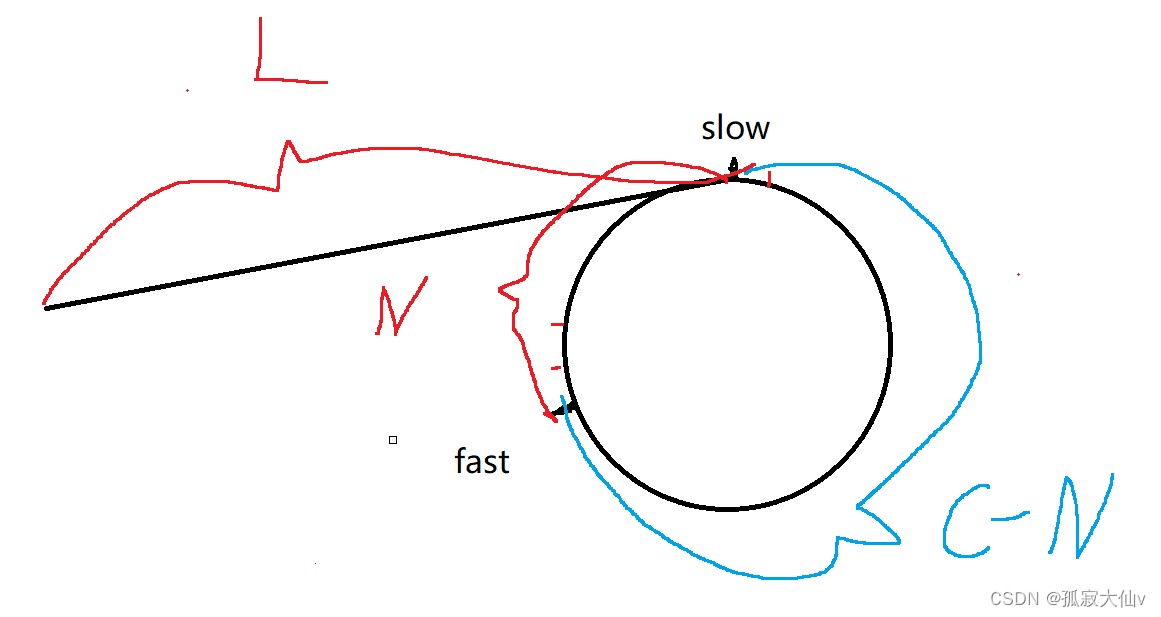
考虑长度为4时如图所示,贪心策略表示为左,(a, b) + (c, d)表示为右,那么左边的结果说明 c >= a >= d,那么显然左边的策略更优

-
以此类推,可以推广到长度为n
-
最小值:O(n^2)
最大值:O(n^2)
总体:O(n^2)
AC代码
#include <bits/stdc++.h>
const int N = 205;
int n, s[N], f[N][N], g[N][N], p[N][N];
int main() {
memset(f, 0x3f, sizeof f);
std::cin >> n;
for (int i = 1; i <= n; i ++)
std::cin >> s[i], s[i + n] = s[i];
for (int i = 1; i <= n * 2; i ++)
s[i] += s[i - 1], f[i][i] = g[i][i] = 0, p[i][i] = i;
for (int len = 2; len <= n; len ++) {
for (int l = 1, r; (r = l + len - 1) <= 2 * n; l ++) {
for (int k = p[l][r - 1]; k <= p[l + 1][r]; k ++)
if (f[l][r] > f[l][k] + f[k + 1][r] + s[r] - s[l - 1])
f[l][r] = f[l][k] + f[k + 1][r] + s[r] - s[l - 1], p[l][r] = k;
g[l][r] = std::max(g[l][r - 1], g[l + 1][r]) + s[r] - s[l - 1];
}
}
int mi = 1e9, ma = 0;
for (int i = 1; i <= n; i ++) mi = std::min(f[i][i + n - 1], mi), ma = std::max(ma, g[i][i + n - 1]);
std::cout << mi << '\n' << ma;
return 0;
}
3.2 P4767 [IOI2000] 邮局
原题链接
[P4767 IOI2000] 邮局 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路分析
n 个村庄建立 m 个邮局, 很经典的dp模型
定义状态f(i, j)为前i个村庄建立j个邮局的最小代价,状态满足不重不漏,考虑状态转移
f
(
i
,
j
)
=
m
i
n
{
f
(
k
,
j
−
1
)
+
w
(
k
+
1
,
i
)
}
f(i, j) = min\{f(k, j - 1) + w(k + 1, i)\}
f(i,j)=min{f(k,j−1)+w(k+1,i)}
意即,前k个村庄由这j - 1个邮局掌控, [k + 1, i]由第j个邮局掌控, w(k + 1, i)为[k + 1, i]建一个邮局的最小代价,这个很容易,建在中位数即可
我们考虑暴力计算w是O(n^3)就别想了,肯定能优化
w
(
i
,
j
)
=
w
(
i
,
j
−
1
)
+
p
o
s
(
i
)
−
p
o
s
(
(
i
+
j
)
/
2
)
w(i, j) = w(i, j - 1) + pos(i) - pos((i + j) / 2)
w(i,j)=w(i,j−1)+pos(i)−pos((i+j)/2)
怎么个事?
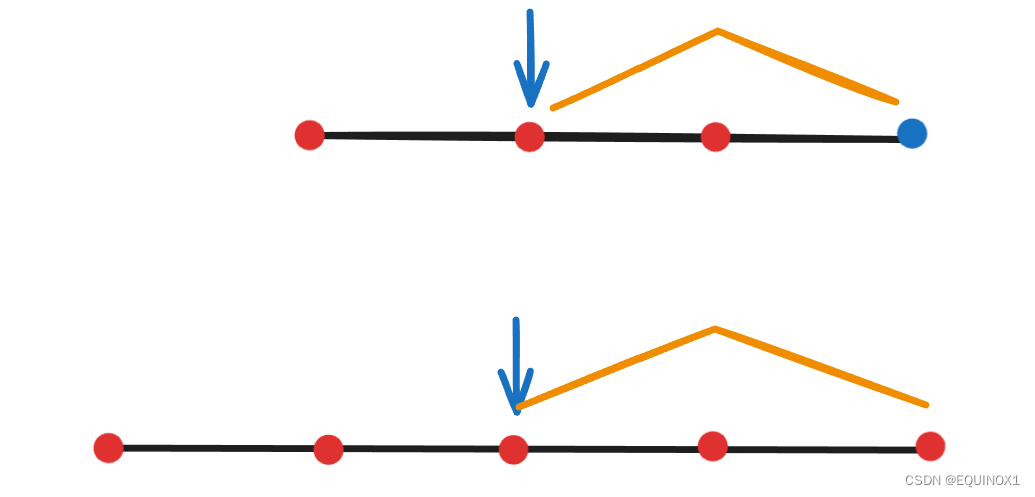
上面是插入后无论为偶数个点还是奇数个点,对于前面的点来说,它们的代价不变,我们只需加上新插入点的代价
(如果插入后原来的邮局需要右移,那么对于前面区间来说代价是不变的,而调整后的邮局位置总是偶数情况下的左中位点或者奇数情况下的中位点)
那么可以写出下面这个TLE代码
70分朴素代码
#include <bits/stdc++.h>
const int N = 305, M = 35;
int n, m, pos[N];
int f[N][M], w[N][N];
//[1, i] build j
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
std::cin >> n >> m;
for(int i = 1; i <= n; i ++) std::cin >> pos[i];
for(int i = 1; i <= n; i ++)
for(int j = i + 1; j <= n; j ++)
w[i][j] = w[i][j - 1] + pos[j] - pos[(i + j) / 2];
for(int j = 1; j <= m; j ++) {
for(int i = j; i <= n; i ++) {
for(int k = j - 1; k < i; k ++)
f[i][j] = std::min(f[i][j], f[k][j - 1] + w[k + 1][i]);
}
}
std::cout << f[n][m];
return 0;
}
形式看起来可以四边形不等式优化,看看是否真的可以——w是否满足四边形不等式?
w(i, j + 1) + w(i + 1, j) - w(i, j) - w(i + 1, j + 1)
= pos(j + 1) - pos((i + j + 1) / 2) - pos(j + 1) + pos((i + j + 2) / 2)
= pos((i + j + 2) / 2) - pos((i + j + 1) / 2)
> 0
所以可以优化!!!
p(i, j - 1) <= p(i, j) <= p(i + 1, j)
由于我们状态转移由前一列转移,所以我们外层是枚举j,所以p(i, j - 1)已知
但是p(i + 1, j)是下一行的内容,这说明我们在枚举i要倒序枚举,由于边界用到n + 1行,所以相应的初始化p(n + 1, i) = n
AC代码
f[i][j] 写成 f[i][i]debug了半天
#include <bits/stdc++.h>
const int N = 3005, M = 305;
int n, m, pos[N];
int f[N][M], w[N][N], p[N][N];
//[1, i] build j
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
std::cin >> n >> m;
for(int i = 1; i <= n; i ++) std::cin >> pos[i];
for(int i = 1; i <= n; i ++)
for(int j = i + 1; j <= n; j ++)
w[i][j] = w[i][j - 1] + pos[j] - pos[(i + j) / 2];
for(int i = 1; i <= m; i ++) p[n + 1][i] = n;
for(int j = 1; j <= m; j ++)
for(int i = n; i >= j; i --)
for(int k = p[i][j - 1]; k <= p[i + 1][j]; k ++)
if (f[i][j] > f[k][j - 1] + w[k + 1][i])
f[i][j] = f[k][j - 1] + w[k + 1][i], p[i][j] = k;
std::cout << f[n][m];
return 0;
}
3.3 Optimal Binary Search Tree
原题链接
Optimal Binary Search Tree - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路分析
定义状态f(l, r)为区间[l, r]构造出最优二叉搜索树的代价
那么枚举根节点k
有f(l, r) = min(f(l, r), f(l, k - 1) + f(k + 1, r) + s(r) - s(l - 1) - w(k))
其中w(i)为第i个元素的权值,s(i)为前i个元素的前缀和
有如下O(n^3)转移方程
#include <bits/stdc++.h>
const int N = 255;
int n;
int f[N][N], w[N], s[N];
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
while(std::cin >> n) {
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i ++) std::cin >> w[i], s[i] = w[i] + s[i - 1], f[i][i] = 0;
for(int len = 2; len <= n; len ++)
for(int l = 1, r; (r = l + len - 1) <= n; l ++)
for(int k = l; k <= r; k ++)
f[l][r] = std::min(f[l][r], (l <= k - 1) * f[l][k - 1] + (k + 1 <= r) * f[k + 1][r] + s[r] - s[l - 1] - w[k]);
std::cout << f[1][n] << '\n';
}
return 0;
}
考虑四边形不等式优化和石子合并其实一样的,直接改写代码就行
AC代码
#include <bits/stdc++.h>
const int N = 255;
int n;
int f[N][N], p[N][N], w[N], s[N];
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
while(std::cin >> n, n) {
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i ++)
std::cin >> w[i], s[i] = w[i] + s[i - 1],
f[i][i] = f[i + 1][i] = f[i][i - 1] = 0, p[i][i] = i;
for(int len = 2; len <= n; len ++)
for(int l = 1, r; (r = l + len - 1) <= n; l ++)
for(int k = p[l][r - 1]; k <= p[l + 1][r]; k ++) {
int t = f[l][k - 1] + f[k + 1][r] + s[r] - s[l - 1] - w[k];
if(f[l][r] > t)
f[l][r] = t, p[l][r] = k;
}
std::cout << f[1][n] << '\n';
}
return 0;
}